Área

Integración: La integral definida

Área

El área de la superficie #\orange S# por encima del eje #x# y limitada por la gráfica de #\blue{f}#, las rectas #x=a# y #x=b# es igual a

\[\int_a^b \blue f(x) \; \dd x\]

Plaatje hoofdblok

El área de un punto de partida fijo hasta #x# por debajo de #\blue f# y por encima del eje #x# se llamará #\orange A(x)# (ver la figura de la derecha).

Probaremos primero que #\orange A(x)# es una primitiva de #\blue f#. Para probar que mostramos que #A'(x)=\blue{f}(x)#.

De la definición derivada:

\[A'(x)=\frac{\orange A(x+h)-\orange A(x)}{h} \text{ con } h \to 0\]

Plaatje 1

El área de #\orange A(x+h)-\orange A(x)# se puede ver en la figura de la derecha. Para pequeños valores de #h# la parte morada se puede aproximar a un rectángulo con lados #h# y #\blue f(x)#. Esto significa

\[\orange A(x+h)-\orange A(x) \approx \blue f(x) \cdot h\]

Al dividir ambos lados entre #h#, encontramos

\[\blue f(x) \approx \frac{\orange A(x+h)-\orange A(x)}{h}\]

Cuando dejamos #h \to 0#, efectivamente vemos que \[\blue f(x)=A'(x)\]

Con esto hemos probado que #\orange A(x)# es una primitiva de #\blue f#.

image 2

Finalmente, vemos en la figura de la derecha la situación en la que queremos saber el área de #a# a #b# por debajo de #\blue f#. Podemos ver que esta área es igual a #\orange A(b)-\orange A(a)#.

Dado que #\orange A(x)# es una primitiva de #\blue f(x)#, usando la definición de la integral definida, el área de #a# a #b# por debajo #f# es igual a: \[\orange A(b)-\orange A(a)=\int_a^b \blue f(x) \; \dd x\]

image 3

Aplicación en física

Al igual que con la diferenciación, la integración tiene muchas aplicaciones en la vida real. Por ejemplo, podemos usarla para calcular la distancia recorrida. Imagina que un avión despega y por los primeros #20# segundos tiene una velocidad de #v(t)=\frac{1}{2}t^2#, entonces el área de la superficie delimitada en #v(t)# y las rectas #t=0# y #t=20# es igual a la distancia recorrida.

\[\int_{0}^{20}v(t)\, \dd t=\int_{0}^{20}\frac{1}{2}t^2\, \dd t =\left[\frac{1}{6}t^3\right]_{0}^{20}=\frac{4000}{3}\]

Por lo tanto, el avión viajó aproximadamente #1330# metros en los primeros #20# segundos.

Ahora hemos visto cómo calcular el área de una superficie por encima del eje #x#, pero de la misma manera podemos calcular una superficie por debajo del eje #x#.

El área de la superficie #\orange S# que se encuentra por debajo del eje #x# y está delimitada en la gráfica de #\blue{f}#, las rectas #x=a# y #x=b# es igual a:

\[-\int_a^b \blue f(x) \; \dd x\]

main image 2

De la misma manera que hemos mostrado para una superficie por encima del eje #x#, podemos demostrar que #\int_a^b \blue f(x) \; \dd x# es igual al #-(\text{área})#.

Finalmente presentaremos un procedimiento de cómo calcular el área delimitada por la gráfica de #\blue f#, el eje #x# y las rectas #x=a# y #x=b#. Aquí, el área puede estar en la parte por encima y en la parte por debajo de la gráfica.

	Procedimiento	Ejemplo
	Determina el área de una superficie delimitada por la gráfica #\blue f#, el eje #x# y las rectas #x=a# y #x=b#.	El área delimitada por #\blue f(x)=-(x-3)^2+4#, el eje #x# y #x=0# y #x=6#
Paso 1	Determina los ceros de la gráfica de #\blue f# entre #x=a# y #x=b#. Llamaremos estos ceros #x_1#, #x_2#, #\ldots#, #x_n# si hay #n# ceros.	#x_1=1#, #x_2=5#
Paso 2	Por cada intervalo #\ivco{a}{x_1}#, #\ivoo{x_1}{x_2}#, #\ldots#, #\ivoc{x_n}{ b}# determina si los valores #y# de #f# son positivos o negativos.	\[f(x)\begin{cases}\lt0&\text{también } x \text{ en } \ivco{0}{1}\\ \gt0&\text{si } x \text{ en } \ivoo{1}{5} \\ \lt 0 &\text{si } x \text{ en } \ivoc{5}{6}\end{cases} \]
Paso 3	El área de la superficie es igual a: \[\pm \int_a^{x_1} \blue f (x)\; \dd x \pm \int_{x_1}^{x_2} \blue f (x)\; \dd x \pm \ldots \pm \int_{x_n}^{b} \blue f(x) \; \dd x \] Aquí, tenemos un signo más adelante de la integral si #f# es positivo para ese dominio y un signo menos si #f# es negativo.	\[\begin{array}{c}-\int_{0}^{1} (x-3)^2+4 \; \dd x \\ + \int_{1}^{5} (x-3)^2+4 \; \dd x \\ - \int_{5}^6 (x-3)^2+4 \; \dd x\end{array}\]
Paso 4	Calcula las integrales definidas y determina el área.	#\frac{46}{3}#

Gráfica

En la siguiente figura, el área de la parte de color naranja es la que hemos calculado en el ejemplo.

Plaatje stappenplan

La siguiente figura muestra la gráfica de la función #f(x)=x^2-7\cdot x+6# dibujada para #x\in\ivcc{1}{9}#. La región delimitada por la función #f# y el eje #x# es de color gris.

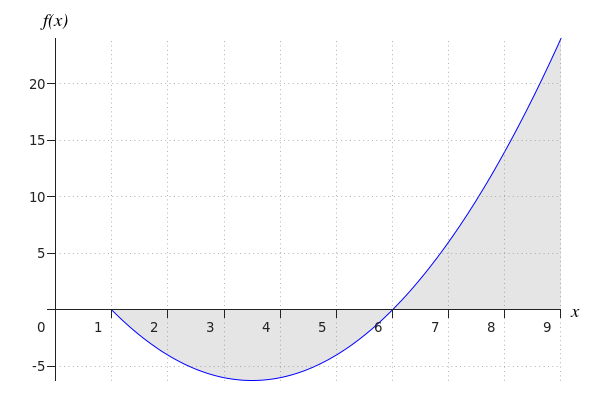
Calcula el área del dominio delimitado.
Da tu respuesta como fracción simplificada.

#\frac{157}{3}#

Paso 1	El único cero de #f(x)=x^2-7\cdot x+6# entre #x=1# y #x=9# es #x_1=6#. El otro cero del polinomio es #x=1#, pero esto no importa para el cálculo.
Paso 2	Para #[1,6)#, #f(x)# es negativo, para #[6,9)# #f(x)# es positivo.
Paso 3	El área de la superficie es igual a \[-\int_{1}^{6} f(x) \, \dd x+ \int_{6}^{9}f(x) \, \dd x\]
Paso 4	Calculamos las integrales definidas. \[\begin{array}{rcl}\displaystyle \int_{1}^{6} x^2-7\cdot x+6 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}-{{7\cdot x^2}\over{2}}+6\cdot x\right]_{1}^{6}\\ &&\phantom{xxx}\blue{\text{definición de integral definida}}\\ &=&\displaystyle -18 - {{17}\over{6}}\\ &&\phantom{xxx}\blue{\text{entrada de límites y se simplifica}}\\ &=&\displaystyle -{{125}\over{6}}\\ &&\phantom{xxx}\blue{\text{simplificado}} \end{array}\] \[\begin{array}{rcl}\displaystyle \int_{6}^{9} x^2-7\cdot x+6 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}-{{7\cdot x^2}\over{2}}+6\cdot x\right]_{6}^{9}\\ &&\phantom{xxx}\blue{\text{definición de integral definida}}\\ &=&\displaystyle {{27}\over{2}} +18\\ &&\phantom{xxx}\blue{\text{entrada de límites y se simplifica}}\\ &=&\displaystyle {{63}\over{2}}\\ &&\phantom{xxx}\blue{\text{simplificado}} \end{array}\] Lo ingresamos y así encontramos el área que buscamos \[\begin{array}{rcl}\displaystyle -\int_{1}^{6} f(x) \, \dd x+ \int_{6}^{9}f(x) \, \dd x&=&\displaystyle -(-{{125}\over{6}})+{{63}\over{2}}\\&=&\displaystyle \frac{157}{3} \end{array}\]

Nuevo ejemplo