Diferenciación: La derivada
 La línea tangente
La línea tangente
Considera la gráfica de la función #f(x)=2\sqrt{x}# representada a la derecha. Podemos dibujar una línea recta #\orange{k}# para el cociente diferencial en #\blue{a}# con una diferencia #\green{h}# que se desplaza a través de los dos puntos #\rv{\blue{a},f(\blue{a})}# y #[\blue{a}+\green{h},f(\blue{a}+\green{h})]#, como hicimos con las funciones lineales.
Si tomamos una #\green{h}# menor, vemos que la recta #\orange{k}# alrededor del punto #\blue{a}# es cada vez más similar a la gráfica.
La línea tangente es un concepto importante. Esta es una línea recta que pasa a través de un punto en una gráfica que tiene la misma pendiente que la gráfica en ese punto.
La línea tangente
Llamamos a una recta que toca una gráfica en el punto #\blue{P}# la línea tangente en ese punto #\blue{P}#. Esto significa que la pendiente de la línea tangente y de la gráfica en el punto #\blue{P}# son iguales, lo que hace que parezcan muy similares alrededor del punto #\blue{P}#.
La línea tangente #\orange{k}# es una función lineal #\orange{k(x)}=\orange{ax+b}#. Aquí, la pendiente #a# es igual a la pendiente de la gráfica en el punto #\blue{P}#.
En la imagen de la derecha, puedes mover el punto #\blue{P}# por tu cuenta para ver cuál es la línea tangente #\orange{k}# a la gráfica #f(x)=\tfrac{1}{5}x^3-2x# en el punto #\blue{P}#.
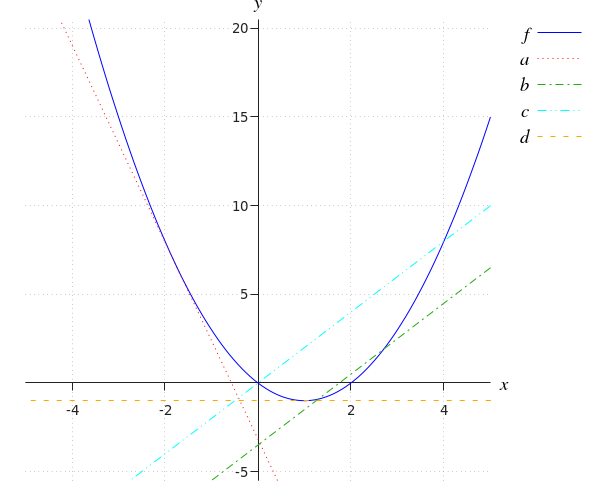
¿Cuáles de estas rectas son líneas tangentes de la gráfica #f(x)#?

Or visit omptest.org if jou are taking an OMPT exam.



