Funciones exponenciales y logaritmos: Funciones logarítmicas
Gráfica de la función logarítmica
Previamente, observamos la función exponencial y su gráfica correspondiente. Ahora estudiaremos la gráfica de la función logarítmica. Veremos algunos puntos en común interesantes entre esta gráfica y la gráfica de la función exponencial.
Una función de la forma \[f(x)=\log_\blue{a}\left(x\right)\]con #\blue{a}>0# se denomina una función logarítmica.
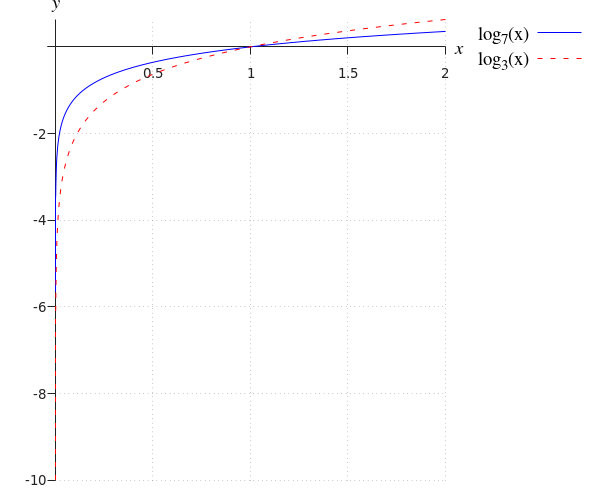
La asíntota de la gráfica es el eje #y#. El logaritmo no está definido para #x=0#, pero se define para números positivos muy cercanos a cero.
Según el valor de #\blue{a}#, la gráfica es creciente o decreciente. Si #\blue{a}>1#, la gráfica es creciente. Si #0<\blue{a}<1#, la gráfica es decreciente.
Notamos que el dominio de la función logarítmica es solo el eje #x# positivo y su rango es todo el eje #y#.
Los valores dados de los números de base son irrelevantes: la gráfica de #\log_a(x)# siempre se moverá a través del punto #\rv{1,0}#, siempre y cuando #a# sea positivo, ya que #a^0=1#.
Or visit omptest.org if jou are taking an OMPT exam.
