Trigonometría: Funciones trigonométricas
 Funciones trigonométricas
Funciones trigonométricas
El seno, el coseno y la tangente no solo se usan en ángulos, sino que también se pueden usar como una función.
La función seno #f(x)=\sin(x)# es la función que suma el seno de #x# a cada número #x#.
Como hemos visto en el círculo unitario, la función se repite cada #2 \pi#. Por lo tanto, llamamos a la función seno una función periódica con #\blue{\text{periodo}}# #2 \pi#.
La función también tiene un #\green{\text{equilibrio}}#. Este es el medio de la función, o el valor #y# que se encuentra exactamente entre el punto más alto y el más bajo. Para la función seno, es #0#.
Finalmente, la #\purple{\text{amplitud}}# de la función es igual a #1#. Esto significa que el valor entre el equilibrio y el punto más alto (o el punto más bajo) es igual a #1#.
La función coseno #f(x)=\cos(x)# es la función que suma el coseno de #x# radianes a cada número en #x#.
Al igual que la función seno, la función coseno es una función periódica. Esto también tiene #\blue{\text{periodo}}# #2\pi#.
El #\green{\text{equilibrio}}# es igual a #0#.
Además, la #\purple{\text{amplitud}}# de la función es igual a #1#.
Cuando comparamos la función coseno con la función seno, vemos que las gráficas son muy similares. Cuando movemos la función coseno a la derecha en #\frac{\pi}{2}#, tenemos la función seno.
La función tangente #f(x)=\tan(x)# es la función que suma la tangente de #x# radianes a cada número #x#.
Al igual que las funciones seno y coseno, la función tangente es una función periódica. El #\blue{\text{periodo}}# es igual a #\pi#.
Las asíntotas verticales de la función tangente son #x=\frac{\pi}{2}+k \cdot \pi#, donde #k# es un número entero, en cuanto a los valores de #x# #\frac{\pi}{2}#, #\frac{3 \pi}{2}# y #\frac{5 \pi}{2}#, pero también para #\frac{-3 \pi}{2}#.
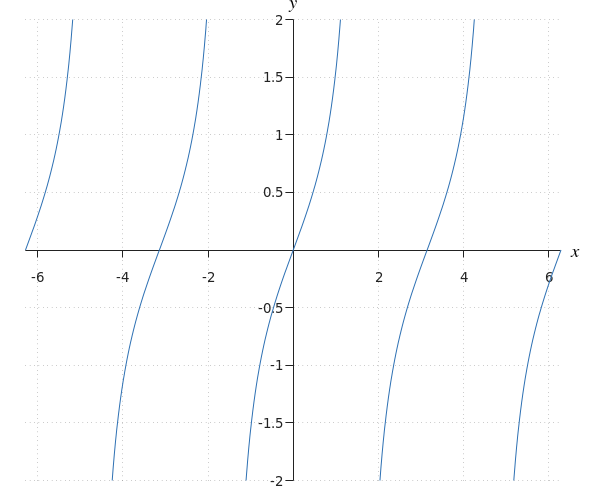
¿A qué función pertenece esta gráfica?
#f(x)=\tan \left(x\right)#
Vemos una función con periodo #\pi# y asíntotas verticales #x=\tfrac{\pi}{2}#, #x=\tfrac{3 \pi}{2}#, #x=-\tfrac{\pi}{2}# y #x=-\tfrac{3 \pi}{2}#. Esto significa que la función es igual a #f(x)=\tan \left(x\right)#.

Or visit omptest.org if jou are taking an OMPT exam.



