Vectores

Geometría: Curvas paramétricas

Vectores

El concepto de flechas dirigidas de cierta longitud en el plano se puede precisar utilizando vectores. Los vectores son objetos con longitud (o magnitud) y dirección. Empezamos con la noción de un "vector de desplazamiento".

Supongamos que #\blue A# y #\green B# son puntos en el plano. Define el vector de desplazamiento #\vec{\blue A \green B}# como la flecha (recta) que comienza en #\blue A# y termina en #\green B#.

Nosotros decimos que #\blue A# es el punto de partida (o inicial) de #\vec{ \blue A \green B}# y #\green B# es el punto final (o terminal) de #\vec{ \blue A \green B}#.

El origen se denota con la letra #O#

Ejemplo

La siguiente imagen indica #\vec{O \green B}# donde #\green B=\rv{1,2}#.

Se pueden sumar dos vectores de desplazamiento siempre que el punto final de uno coincida con el punto inicial del otro.

Supongamos que #\blue A, \green B# y #\orange C# son tres puntos en el plano. Define la suma de #\vec{\blue A \green B}# y #\vec{ \green B \orange C}# como

\[ \vec{\blue A \green B} + \vec{ \green B \orange C} = \vec{ \blue A \orange C }\]

Un vector de desplazamiento siempre se puede "mover". Esto da la noción de un vector. Intuitivamente, un vector es un vector de desplazamiento sin ningún punto de partida especificado.

Un vector #\blue{\vec{x}}# es una flecha en el plano que se puede reposicionar, sin girar o estirar/encoger, al vector de desplazamiento #\vec{OA}# por algún punto #A# en el plano.

Si #A=\rv{x_1,x_2}#, denotamos el vector #\blue{\vec{x}}# por #\cv { x_1 \\x_2 }#.

Ten en cuenta que hay múltiples representaciones del mismo vector. La imagen muestra varias representaciones del vector #\cv{1\\2}#.

Ejemplo

Como se dijo, es común reposicionar nuestros vectores a un vector de la forma #\vec{OA}#. En este caso también podemos decidir escribir #A=[x_1,x_2]# para el vector

La longitud de un vector se puede calcular usando el teorema de Pitágoras.

Dado un vector #\blue{\vec{x}}=\cv{ \green{x_1}\\ \orange{x_2} }#, la longitud del vector, denotada por #\| \blue{\vec{x}} \|#, es dada por

\[\| \blue{\vec{x}} \| = \sqrt{\green{x_1}^2+\orange{x_2}^2}\]

Ejemplo

El largo de #\blue{\vec{x}}=\cv{\green{1}\\ \orange{2}}# es dado por \[\|\blue{\vec{x}}\|=\sqrt{\green 1^2+ \orange 2^2}=\sqrt{5}\]

Teorema de Pitágoras

Como se mencionó, esta longitud se calcula usando el teorema de Pitágoras. Considera la imagen de la derecha.

Vemos un triángulo rectángulo con lados #\green{x_1}# y #\orange{x_2}#. La longitud de la hipotenusa está dada por #\sqrt{\green{x_1}^2 + \orange{x_2}^2 }#.

Esto corresponde a la longitud del vector #\blue{\vec{x}}#

Imagen

Observa que la longitud de un vector siempre es positiva, excepto el vector cero, que tiene una longitud cero.

Sumar vectores es considerablemente más fácil que sumar vectores de desplazamiento. Por ejemplo, dos vectores cualesquiera pueden sumarse independientemente, mientras que dos vectores de desplazamiento deben alinearse para poder sumarse. También podemos definir la "multiplicación escalar".

Supongamos que #\blue{\vec{x}} =\blue{\cv{x_1\\x_2}}# y #\green{\vec{y}}=\green{\cv{y_1\\y_2}}# son dos vectores y #c# es un número real. Definimos la suma de #\blue{\vec{x}}# y #\green{\vec{y}} # como \[\blue{\vec{x}}+\green{\vec{y}}=\cv{\blue{x_1}+\green{y_1}\\\blue{x_2}+\green{y_2}}\]

y la multiplicación escalar #\orange{c} \cdot \blue {\vec{x}}#

\[\orange{c} \cdot \blue{\vec{x}}=\cv{\orange{c}\cdot \blue{x_1}\\ \orange{c}\cdot \blue{ x_2}}\]

Ejemplo

La geometría de sumar dos vectores se visualiza mejor con la llamada regla de la cabeza y la cola. Esta regla establece que dados dos vectores, #\blue{\vec{x}}# y #\green{\vec{y}}#, la suma de estos dos se obtiene posicionando #\green{\vec{y}}# en el punto final de #\blue{\vec{x}}#. Esto se puede ver en la imagen.

Imagen de múltiplo escalar

Múltiplo escalar

Esta es una imagen del múltiplo escalar de un vector. Puedes ajustar el valor de #\orange c# usando el control deslizante en la esquina superior derecha.

Ten en cuenta que la dirección de #\blue {\vec{x}} # cambia solo si #\orange c# es negativo

Imagen

Vector de desplazamiento

Supongamos que #\blue A = \rv{\blue{x_1},\blue{x_2}}# y #\green B = \rv{\green{y_1},\green{y_2}}# son puntos en el plano. Entonces sabemos que \[\vec{O\blue{A}}+ \vec{\blue A \green B} = \vec{O\green{B}}\]

Por lo tanto, el vector de desplazamiento #\vec{\blue A \green B}# se puede calcular como la diferencia de #\vec{O\green{B}}# y #\vec{O\blue{A}}#, \[ \begin{array}{rcl}
\vec{\blue A \green B} &=& \vec{O\green{B}} - \vec{O\blue{A}} \\
&=& \cv{\green{y_1 \\ y_2}} - \cv{\blue{x_1 \\ x_2}} \\
&=& \cv{\green{y_1} - \blue{x_1} \\ \green{y_2} - \blue{x_2} }
\end{array}\]

Ejemplo

#\blue{A} = \rv{\blue 1,\blue 2}# y #\green{B} = \rv{\green 4, \green 3}# entonces \[\vec{\blue A \green B} = \cv{\green 4-\blue 1 \\ \green 3-\blue 2} = \cv{3 \\ 1} \]

Según los vectores #\vec{u}=\rv{12,12}# y #\vec{v}=\rv{-7,9}#, calcula el vector

\[ 3\cdot \vec{u}-3\cdot \vec{v}\tiny.\]

\(3\cdot\vec{u}-3 \cdot \vec{v}=\) # \left[ 57 , 9 \right]#

Esto se deduce del siguiente cálculo:
\[\begin{array}{rcl} 3\cdot\vec{u}-3\cdot\vec{v}&=&3\cdot\rv{12,12}-3\cdot\rv{-7,9}\\
&&\qquad \blue{\text{definiciones }\vec{u}, \vec{v}}\\
&=&\rv{3\cdot 12, 3\cdot 12}+\rv{-3\cdot-7, -3\cdot 9}\\
&&\qquad \blue{\text{multiplicación por coordenada}}\\
&=&\rv{36, 36}+\rv{21, -27}\\
&&\qquad \blue{\text{se simplificó}}\\
&=&\rv{36+21, 36-27}\\
&&\qquad \blue{\text{adición por coordenada}}\\
&=&\rv{57,9}\\
&&\qquad \blue{\text{se simplificó}}\end{array}\]

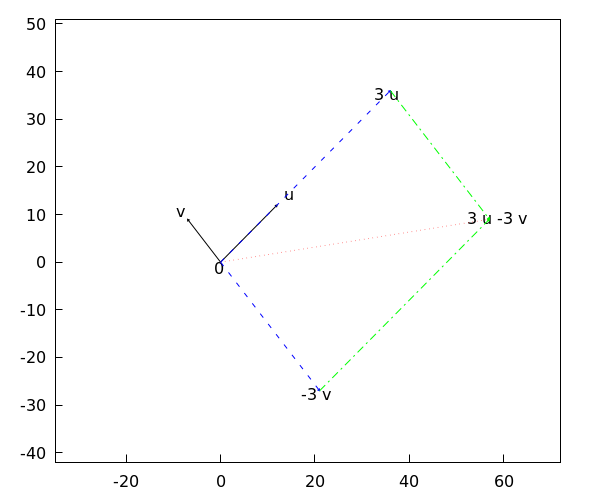
La siguiente figura muestra los vectores #\vec{u}# y #\vec{v}# dibujados en negro, los vectores #3\cdot \vec{u}# y #-3\cdot\vec{v}# en rectas punteadas azules y el vector #3\cdot\vec{u}-3\cdot\vec{v}# en una recta punteada roja.

Nuevo ejemplo