Componer la ecuación de una recta

Sistemas de ecuaciones lineales: Una ecuación de una recta

Componer la ecuación de una recta

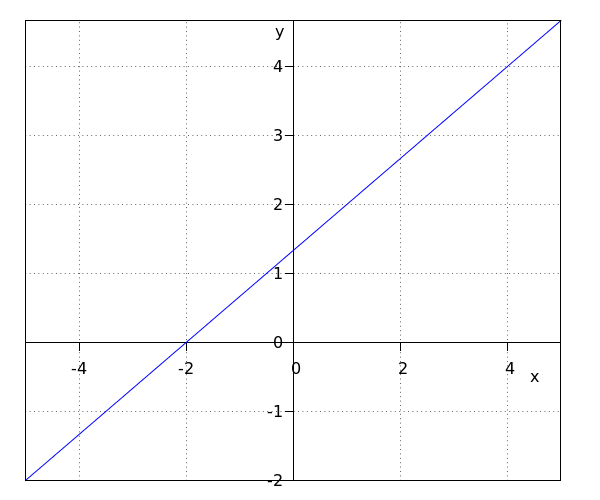
Gráfica

geogebra plaatje

Componer una ecuación lineal que pase a través de dos puntos

	Procedimiento	Ejemplo
	Componer una ecuación de la recta que pase a través de dos puntos #A=\rv{\blue{x_A}, \blue{y_A}}# y #B=\rv{\green{x_B}, \green{y_B}}#.	Supongamos que # A=\rv{\blue2, \blue5}# y #B=\rv{\green4,\green2}#.
Paso 1	Determina la pendiente #a# con ayuda de la fórmula: \[a=\frac{\green{y_B}-\blue{y_A}}{\green{x_B}-\blue{x_A}}\]	#\begin{array}{rcl}a&=&\dfrac{\green{y_B}-\blue{y_A}}{\green{x_B}-\blue{x_A}}\\ &=&\dfrac{\green2-\blue5}{\green4-\blue2}\\ &=&-\dfrac{3}{2}\end{array}#
Paso 2	La ecuación es de la forma #y=a \cdot x+b# con #a# del paso 1 y #b# como un número indefinido.	#y=-\dfrac{3}{2} \cdot x+b#
Paso 3	Introduce el punto #A=\rv{\blue{x_A},\blue{y_A}}# en la ecuación del paso 2: \[\blue{y_A}=a \cdot \blue{x_A}+b\]	#\blue5=-\dfrac{3}{2} \cdot \blue2 +b#
Paso 4	Resuelve la ecuación del paso 3 para la incógnita #b#.	#\begin{array}{rcl}-\frac{3}{2} \cdot \blue{2} +b&=&\blue{5} \\ -3+b&=&5 \\ b &=&8 \end{array}#
Paso 5	Usa el valor de #b#: \[y=a \cdot x+b\] encontrado en el paso 4.	#y=-\dfrac{3}{2} \cdot x +8#

Recta horizontal

Una excepción a este procedimiento es la recta horizontal. Esta recta se puede reconocer porque las coordenadas #y# de los dos puntos son iguales. Por lo tanto, esta es una recta que pasa a través de los puntos #A=\rv{x_A,\orange c}# y #B=\rv{x_B,\orange c}#. Esta recta es igual a #y=\orange c#.

Ejemplo

La recta que pasa por los puntos #A=\rv{2,\orange8}# y #B=\rv{6, \orange8}# satisface la ecuación\[y=\orange 8\]

Recta vertical

Una excepción a este procedimiento es la recta vertical. Esta recta se puede reconocer porque las coordenadas #x# de los dos puntos son iguales. Por lo tanto, esta es una recta que pasa a través de los puntos #A=\rv{\orange c, y_A}# y #B=\rv{\orange c, y_B}#. Esta recta es igual a #x=\orange c#.

Ejemplo

La recta que pasa por los puntos #A=\rv{\orange8, 2}# y #B=\rv{\orange8,6}# satisface la ecuación \[x=\orange 8\]

Componer una ecuación con una gráficaCon la ayuda de este procedimiento también podemos componer una ecuación con la gráfica de una recta. Podemos hacer esto leyendo dos puntos convenientes de la gráfica y siguiendo el procedimiento con estos puntos.

Ejemplo

Compondremos una ecuación de la forma #y=a \cdot x +b# para la recta a continuación.

Primero elegiremos dos puntos convenientes, por ejemplo #A=\rv{-2,0}# y #B=\rv{4,4}#. Luego, seguiremos el procedimiento.

Paso 1 La pendiente #a# se calcula con la fórmula: \[a=\frac{4-0}{4--2}=-\frac{4}{6}=\frac{2}{3}\]

Paso 2 Por lo tanto, la ecuación es de la forma #y=\tfrac{2}{3} \cdot x+b#.

Paso 3 Introducimos el punto #A=\rv{-2,0}# en la ecuación del paso 2. Esto nos da: \[0=\tfrac{2}{3} \cdot -2 +b\]

Paso 4 Resolvemos la ecuación del paso 3 y encontramos: #b=\tfrac{4}{3}#.

Paso 5 Por lo tanto, la ecuación es #y=\tfrac{2}{3} \cdot x +\tfrac{4}{3}#.

Pendiente dadaPara componer una ecuación de una recta, es suficiente conocer la pendiente y un punto en la gráfica. Luego comenzamos con el paso 2 del procedimiento e introducimos la pendiente conocida de inmediato.

Determina una ecuación para la línea recta que pasa por #\rv{-2,1}# y tiene una pendiente de #4#.

Escribe tu respuesta en forma de #y=a\cdot x+b# con números adecuados #a# y #b# y con incógnitas #x# y #y#.

#y= 4\cdot x +9 #

Paso 1	La pendiente está dada, y es igual a #4#.
Paso 2	Introducimos la pendiente en la ecuación de una recta #y=a \cdot x+b#. Por lo tanto, la ecuación es de la forma: \[y=4\cdot x+b\] en la que #b# es un número.
Paso 3	Introducimos el punto #\rv{-2,1}# en la ecuación del paso 2. Esto nos da: \[ 1=4\cdot (-2)+b\]
Paso 4	Resolvemos la ecuación del paso 3 por medio de la reducción. \[\begin{array}{rcl} 1&=&4\cdot (-2)+b \\ &&\phantom{xxx}\blue{\text{la ecuación a resolver}}\\ 1&=&-8+b \\ &&\phantom{xxx}\blue{\text{simplificado}}\\ 9&=&b \\ &&\phantom{xxx}\blue{\text{ambos lados menos }-8}\\ \end{array}\] Por lo tanto, encontramos #b=9#.
Paso 5	Ahora introducimos #b=9# en la ecuación del paso 2. Encontramos que la recta está dada por la ecuación: \[y= 4\cdot x +9\]

Nuevo ejemplo