Transformaciones de funciones de potencia con exponentes negativos

Funciones: Funciones fraccionarias

Transformaciones de funciones de potencia con exponentes negativos

Hemos visto la forma de la gráfica de una función de potencia #f(x)=\tfrac{1}{x^n}# con #n \gt 0# y #n# es un número entero. Así como las funciones de potencia de la forma #y=x^n# con #n \gt 0# y #n# es un número entero, podemos transformar estas funciones de potencia.

TransformacionesPodemos transformar la función #f(x)=\frac{1}{x^n}# de tres formas diferentes.

	Transformaciones	Ejemplos
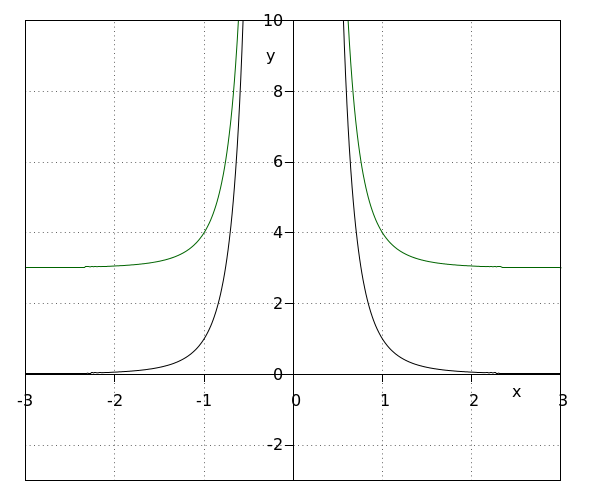
1	Desplazamos la gráfica de #f(x)=\tfrac{1}{x^n}# hacia arriba por #\green q#. La nueva función es \[f(x)=\frac{1}{x^n}+\green q\] Dado que la nueva función se desplaza hacia arriba en #\green q#, el rango se vuelve igual a #\ivoo{\green q}{\infty}# si #n# es par. Si#n# es impar, el rango se vuelve igual a todos los números excepto #\green q#. El dominio permanece igual. Por tanto, la asíntota horizontal es igual a #y=\green q# y la asíntota vertical permanece igual a #x=0#.	que se desplaza #f(x)=\frac{1}{x^4}# hacia arriba por #\green3# da #f(x)=\frac{1}{x^4}+\green3#
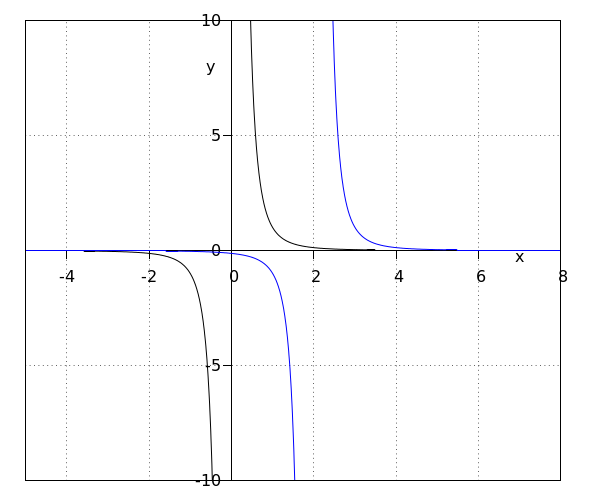
2	Desplazamos la gráfica de #f(x)=\tfrac{1}{x^n}# a la derecha por #\blue p#. La nueva función se convierte en \[f(x)=\frac{1}{\left(x-\blue p\right)^n}\] Dado que la nueva función se desplaza a la derecha por #\blue p#, el dominio se vuelve igual a todos los números excepto #x=\blue p#. El rango permanece igual. Por tanto, la asíntota horizontal permanece igual a #y=0# y la asíntota vertical se vuelve igual a #x=\blue p#.	que se desplaza #f(x)=\frac{1}{x^3}# hacia la derecha por #\blue2# da #f(x)=\frac{1}{\left(x-\blue2\right)^3}#
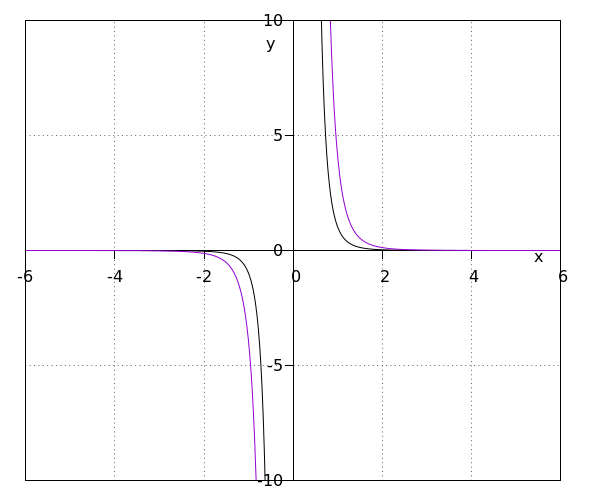
3	Multiplicamos la gráfica de #f(x)=\tfrac{1}{x^n}# por #\purple a# en relación con el eje #x#. La nueva función se convierte en \[f(x)=\frac{\purple a}{x^n}\] Al multiplicar por un número positivo, el dominio, el rango y las asíntotas permanecen iguales a la función original. Por otro lado, si multiplicamos por un número negativo, la función se invierte. Si #n# es impar, el dominio, el rango y las asíntotas permanecen iguales. Ese no es el caso si #n# es par, allí el rango también se invierte a #\ivoo{-\infty}{0}#. El dominio y las asíntotas permanecen iguales.	se multiplica #f(x)=\frac{1}{x^5}# por #\purple4# relativo al eje #x# da #f(x)=\frac{\purple4}{x^5}#

Varias transformacionesTambién podemos realizar varias transformaciones una tras otra.

Por ejemplo: #f(x)=\frac{\purple3 }{\left(x-\blue4\right)^4}# es primero un desplazamiento de #\blue4# al lado derecho y luego una multiplicación por #\purple3# relativo al eje #x#, de la función de potencia con exponente negativo #f(x)=\frac{1}{x^4}#.

SimetríaAl desplazar a la derecha por #\blue p# también vimos un desplazamiento en la asíntota vertical. Esto significa que el eje de simetría de una función par se desplaza hacia la derecha por #x=\blue p#.

Una función de potencia con un exponente negativo impar #n# tiene un punto de simetría en #\rv{0,0}#. Al desplazarse hacia arriba por #\green q#, el punto de simetría también se desplaza hacia arriba por #\green q#. De la misma manera que cuando se desplaza hacia la derecha por #\blue p# el punto de simetría también se desplaza hacia la derecha por #\blue p# al punto #\rv{\blue p, 0}#.

Mira las dos gráficas siguientes.

La fórmula de la gráfica azul es:
\[y={{2}\over{x^6}}\]
¿Cuál es la fórmula de la gráfica verde?

#y=# #{{2}\over{\left(x+2\right)^6}}#

El punto #\rv{1,2}# se encuentra en la gráfica azul, investigaremos dónde está este mismo punto en la gráfica verde. En el gráfico verde, este punto se encuentra en #\rv{-1,2}#.
Por lo tanto, la gráfica verde se obtiene de la azul al desplazar la gráfica azul #2# unidades a la derecha.
Por lo tanto, reemplazamos todas las apariciones de #x# en la fórmula de la gráfica azul #y={{2}\over{x^6}}# por #x+2#. Esto da la siguiente fórmula para la gráfica verde:
\[y={{2}\over{\left(x+2\right)^6}}\]

Nuevo ejemplo