Ecuaciones con funciones de potencia

Funciones: Funciones de potencia

Ecuaciones con funciones de potencia

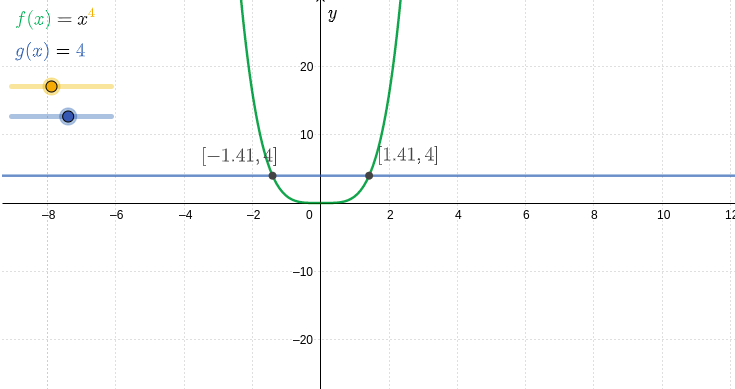
En ecuaciones cuadráticas hemos visto cómo resolver una ecuación #x^2=c#. Con el mismo procedimiento, usaremos raíces de grado mayor para resolver una ecuación #x^n=c#.

Las soluciones de la ecuación #x^\orange{n}=\blue{c}# dependen de los valores de #\orange n# y #\blue c#.

#\blue{c} \gt 0#

#\blue{c}=0#

#\blue{c} \lt 0#

#\orange{n}# es par

Dos soluciones:

#x=-\sqrt[\orange{n}]{\blue{c}} \lor x=\sqrt[\orange{n}]{\blue{c}}#

Una solución:

#x=0#

Ninguna solución

#\orange{n}# es impar

Una solución:

#x=\sqrt[\orange{n}]{\blue{c}}#

Una solución:

#x=0#

Una solución:

#x=\sqrt[\orange{n}]{\blue{c}}#

Poderes fraccionalesRecuerde que hemos visto la siguiente regla con Poderes fraccionales:

\[\sqrt[\orange{n}]{x}=x^{\frac{1}{\orange{n}}}\]

Por lo tanto, también podemos escribir las soluciones con una potencia fraccionaria. Entonces, las soluciones se ven así:

#\blue{c} \gt 0#

#\blue{c}=0#

#\blue{c} \lt 0#

#\orange{n}# es par

Dos soluciones:

#x=-\blue{c}^{\frac{1}{\orange{n}}} \lor x=\blue{c}^{\frac{1}{\orange{n}}}#

Una solución:

#x=0#

Sin soluciones

#\orange{n}# es impar

Una solución:

#x=\blue{c}^{\frac{1}{\orange{n}}}#

Una solución:

#x=0#

Una solución:

#x=\blue{c}^{\frac{1}{\orange{n}}}#

En los ejemplos vemos que puedes reducir muchas ecuaciones a la forma #x^\orange{n}=\blue{c}# y luego resolverlas.

Resuelve #6\, x^{6}+2=6# para #x#.

Da tu respuesta en la forma #x=x_1# o #x=x_1 \lor x=x_2# para los números adecuados #x_1# y #x_2#.

#x=\frac{1}{3}\sqrt[6]{486} \lor x=-\frac{1}{3}\sqrt[6]{486}#

#\begin{array}{rcl}6\, x^{6}+2&=& 6 \\
&&\phantom{xxx}\blue{\text{la ecuación que necesitamos resolver}} \\
6\, x^{6}&=&4 \\
&&\phantom{xxx}\blue{\text{ambos lados menos }2} \\
x^{6} &=& {{2}\over{3}} \\
&&\phantom{xxx}\blue{\text{ambos lados divididos por }6} \\
x=\sqrt[6]{{{2}\over{3}}} &\lor& x=-\sqrt[6]{{{2}\over{3}}} \\
&&\phantom{xxx}\blue{\text{ambos lados tomaron la }6 \text{-ésima raíz}}\\
x=\frac{1}{3}\sqrt[6]{486} &\lor& x=-\frac{1}{3}\sqrt[6]{486}\\
&&\phantom{xxx}\blue{\text{simplificada}} \end{array}#

Nuevo ejemplo