Funciones: Funciones de potencia
 Funciones de potencia
Funciones de potencia
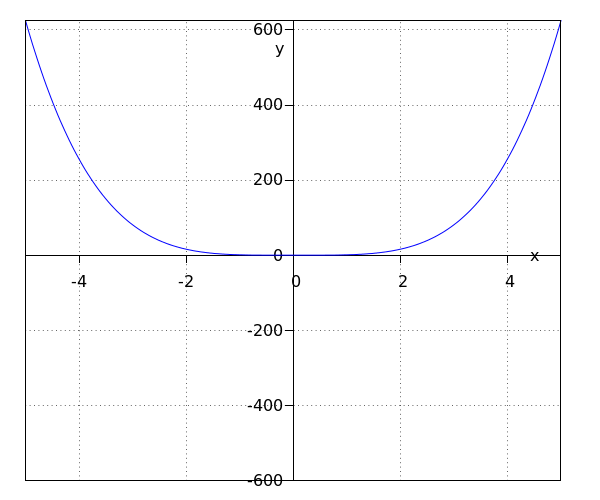
La función #\blue {f}# tiene el intervalo #\ivco{0}{\infty}# como rango.
El eje #y# es el eje de simetría.
El vértice es #\rv{0,0}#.
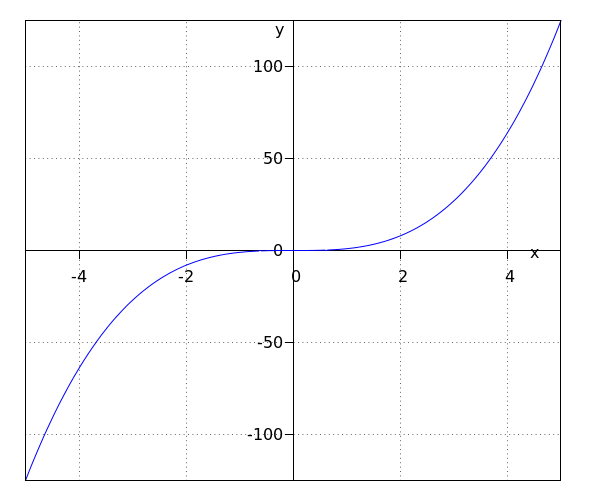
La función #\green{g}# tiene el intervalo #\ivoo{-\infty}{\infty}# como rango.
El punto #\rv{0,0}# es un punto de simetría.
Las dos funciones del ejemplo anterior son funciones de potencia. Es evidente que ambas funciones difieren bastante. Esto tiene que ver con el hecho de que #\blue{f}# es una función de potencia con exponente par y que #\green g# es una función de potencia con exponente impar.
Una función del tipo \[f(x)=\blue{a}x^{\orange{n}}\] con #\blue{a} \ne 0# es una función de potencia.
La gráfica de una función de potencia con #\orange{n} \gt 0# entero pasa por los puntos #\rv{0,0}# y #\rv{1,\blue a}#.
Además, las gráficas de las funciones de potencia difieren dependiendo de si #\orange{n}# es par o impar. Con #\orange{n}# par, la gráfica es simétrica a lo largo del eje #y#. Con #\orange{n}# impar, la gráfica es simétrica a través del punto #\rv{0,0}#.
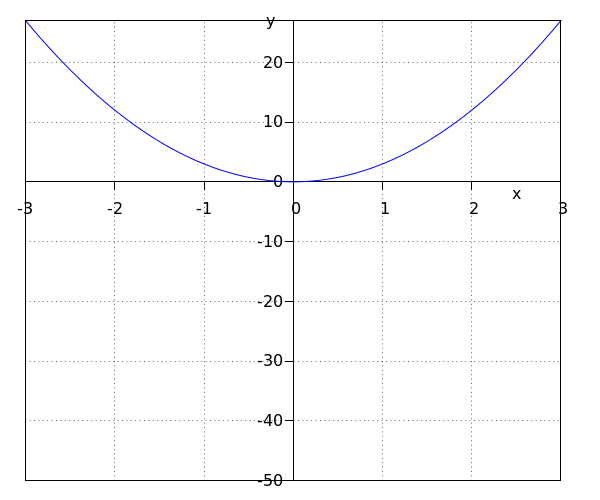
¿Qué sabemos sobre el valor de #n# y #a#?
El valor de #a# es: positivo
La gráfica es simétrica en el eje #y#, por lo tanto, el valor de #n# es par.
El valor #y# es positivo si el valor de #x# es positivo, por lo tanto, el valor de #a# es positivo.

Or visit omptest.org if jou are taking an OMPT exam.



