Ecuaciones de raíz

Funciones: Funciones de potencia y funciones de raíz

Ecuaciones de raíz

A continuación, se muestran ejemplos en los que se debe resolver una ecuación de raíz.

Resuelve #x# en
\[\sqrt{4x+5}=3\]
Da tu respuesta como #x=x_1 \lor x=x_2 \lor \ldots \lor x=x_n#, en el cual #x_1#, #x_2#, #\ldots# #x_n# son números y #n# es el número de soluciones.

#x=1#

\[\begin{array}{rcl}\sqrt{4x+5}&=&3 \\ &&\phantom{xxx}\blue{\text{la ecuación original}}\\
4x+5&=&9 \\ &&\phantom{xxx}\blue{\text{ambos lados al cuadrado}}\\
4x&=& 4 \\ &&\phantom{xxx}\blue{\text{ambos lados menos }5}\\
x&=&1 \\ &&\phantom{xxx}\blue{\text{ambos lados divididos por }4}\end{array}\]

Ahora verificamos las soluciones encontradas #x=1# al ingresarlas en la ecuación:
\[\sqrt{4 \cdot 1+5}=\sqrt{9}=3\]
Por lo tanto, la solución es correcta y la solución de la ecuación es #x=1#.

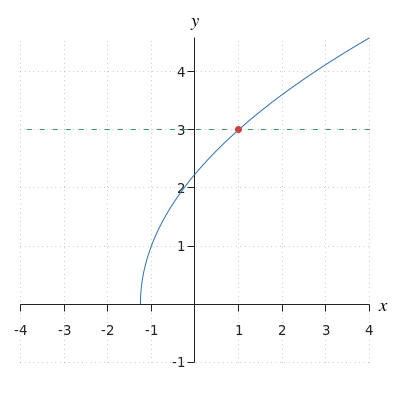
En el siguiente sistema de coordenadas, vemos la gráfica #f(x)=\sqrt{4x+5}# en azul y #g(x)=3# en verde, y su punto de intersección #\rv{1,3}# en rojo.

Nuevo ejemplo

En general, podemos resolver una ecuación de raíz con lo siguiente #4# pasos.

Resolución de ecuaciones de raíz

	Procedimiento Resolvemos una ecuación de raíz para #x#.	Ejemplo #\sqrt{x+4}+4=9#
Paso 1	Aísla la raíz. Esto significa que, mediante la reducción, nos aseguramos de que la raíz sea lo único en un lado de la ecuación.	#\sqrt{x+4}=5#
Paso 2	Toma el cuadrado de ambos lados para deshacerte de la raíz.	#x+4=25#
Paso 3	Resuelve esta ecuación.	#x=21#
Paso 4	Verifica si la solución encontrada es una solución a la ecuación original.	#\sqrt{21+4}+4=9# Por tanto, la solución es correcta.

VerificaciónSe debe verificar la(s) solución(es) porque elevar algo al cuadrado puede generar soluciones que no son soluciones a la ecuación original. Esto se puede ver en el segundo ejemplo en la parte superior de esta página.

Resuelve la siguiente ecuación:
\[\sqrt{6\cdot x+1}=\sqrt{4-2\cdot x}\]
Da tu respuesta en la forma de

#ninguna# si no hay ninguna solución,
#x=x_1# si hay una solución,
#x=x_1\lor x=x_2# si hay dos soluciones,

con los valores correctos para #x_1# y #x_2#.

# x={{3}\over{8}} #

\[\begin{array}{rcl}
\sqrt{6\cdot x+1}&=& \sqrt{4-2\cdot x}\\
&&\phantom{xxx}\blue{\text{ecuación original}}\\

6\cdot x+1&=&4-2\cdot x \\
&&\phantom{xxx}\blue{\text{ambos lados al cuadrado}} \\
8\cdot x&=&3 \\
&&\phantom{xxx}\blue{\text{términos de }x \text{ llevados a la izquierda, términos constantes llevados a la derecha}} \\

x&=&{{3}\over{8}} \\
&&\phantom{xxx}\blue{\text{dividido por el coeficiente de }x} \\
\end{array}\]

Porque hemos tomado el cuadrado, la solución para #x# que encontramos puede no ser una solución a la ecuación original. Por lo tanto, ahora debemos probar la solución que encontramos al ingresarla a la ecuación original.

En el lado izquierdo está:
\[\sqrt{6\cdot \left({{3}\over{8}}\right)+1}={{\sqrt{13}}\over{2}}\]
En el lado derecho está:
\[\sqrt{4-2\cdot \left({{3}\over{8}}\right)}={{\sqrt{13}}\over{2}}\]
izquierda y derecha son iguales, por lo que esta solución es correcta.

En conclusión, la respuesta de la ecuación es # x={{3}\over{8}} #.

Nuevo ejemplo