Funciones: Funciones fraccionarias
Funciones racionales lineales
Una función racional lineal es una función de la forma
\[f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}\]
donde #\blue{a}#, #\green{b}#, #\purple{c}# y #\orange{d}# son números y #x# es una variable.
La gráfica de una función racional lineal es una hipérbola con una asíntota vertical y una horizontal.
Determinamos la asíntota vertical de una función racional lineal #f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}# al hacer el denominador#\purple{c}x+\orange{d}# igual a #0# y resolver esta ecuación.
Por lo tanto, para la asíntota vertical encontramos \[x=-\frac{\orange{d}}{\purple{c}}\]
La asíntota horizontal se puede determinar al observar que para valores muy altos de #x# los números #\green{b}# y #\orange{d}# son insignificantes en relación con los términos con #x#.
Por lo tanto, para la asíntota horizontal tenemos \[y=\frac{\blue{a}x}{\purple{c}x}=\frac{\blue{a}}{\purple{c}}\]
Mira la función #f(x)=\frac{\blue{2}x+\green{-3}}{\purple{4}x+\orange{2}}#
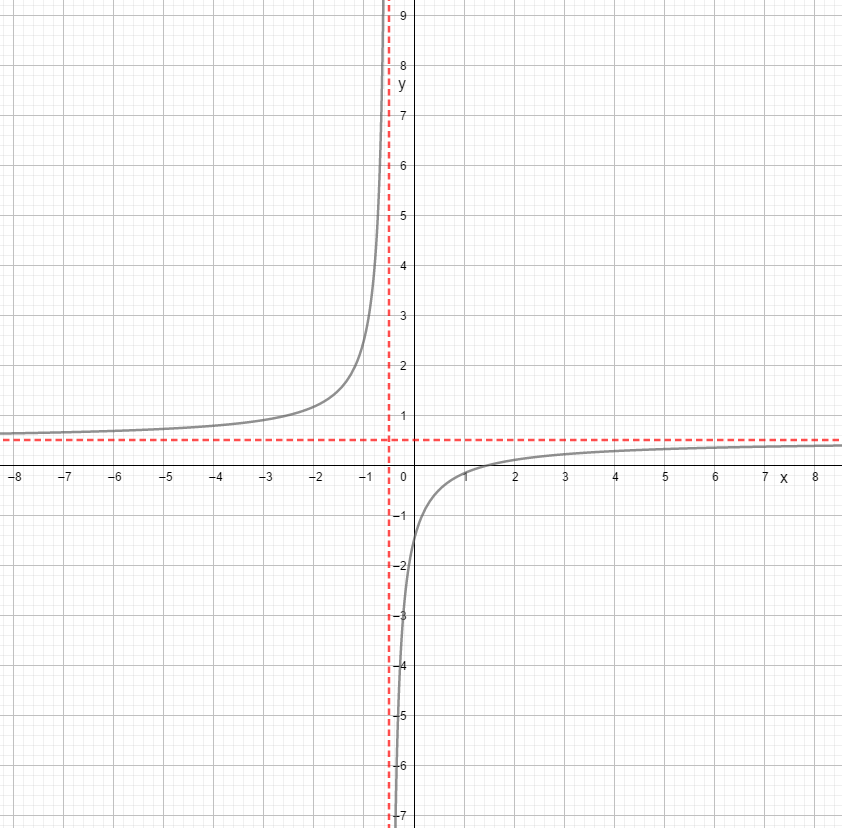
De verticale asymptoot is gelijk aan
\[x=-\frac{\orange{2}}{\purple{4}}=-\frac{1}{2}\]
De horizontale asymptoot is gelijk aan
\[y=\frac{\blue{2}}{\purple{4}}=\frac{1}{2}\]
Or visit omptest.org if jou are taking an OMPT exam.
