Funciones: Funciones fraccionarias
 Asíntotas e hipérbolas
Asíntotas e hipérbolas
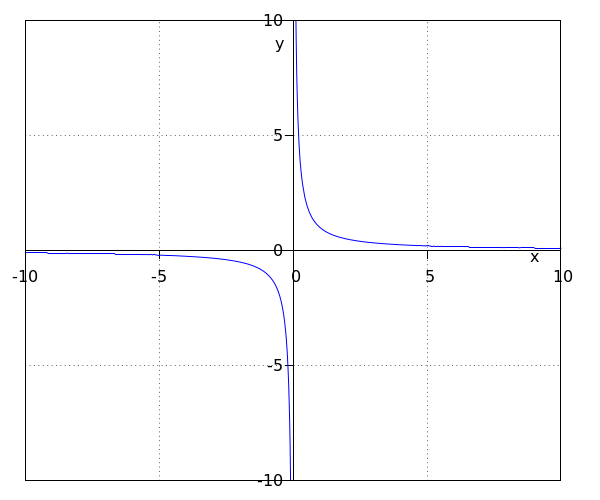
Mira la función #f(x)=\tfrac{1}{x}#. En la gráfica vemos que la función consta de dos ramas . Esto se debe a que #0# no es parte del dominio de la función y, por tanto, #f(0)# no existe. A una gráfica que consta de dos ramas la denominamos #\blue{\textbf{hipérbola}}#.
Vemos que, si #x# se vuelve realmente negativo o si #x# se vuelve realmente positivo, la gráfica se acerca mucho al eje #x#. Sin embargo, el valor de la función nunca llega a ser igual a #0#. Al eje #x#, la línea #y=0#, lo denominamos la #\purple{\textbf{asíntota horizontal}}# de la gráfica.
También vemos que si el valor #x# se acerca a #0# desde el lado negativo, el valor de la función se vuelve arbitrariamente negativo: disminuye sin ningún límite. Por otro lado, si el valor #x# se acerca a #0# desde el lado positivo, #f(x)# se vuelve arbitrariamente positivo. Al eje #y#, la línea #x=0#, lo denominamos la #\green{\textbf{asíntota vertical}}# de la gráfica.
Asíntota e hipérbola
Una asíntota es una línea a la que la función se acerca cada vez más, pero con la cual la gráfica nunca se toca ni coincide.
Una hipérbola es una función que tiene una gráfica que consta de dos partes separadas debido a sus asíntotas. Estas dos partes separadas también se denominan ramas de la gráfica.
La asíntota horizontal es: #y=0#
Después de todo, la asíntota vertical se puede encontrar investigando qué valores para #x# no se pueden ingresar en la función. En una función fraccionaria, el denominador no puede ser igual a #0#. Por tanto, la asíntota vertical es igual a #x=8#.
La asíntota horizontal se puede encontrar ingresando valores muy altos para #x# y luego investigando qué sucede con la función. Si ingresamos valores muy altos de #x#, entonces #x-8# se vuelve muy grande. Luego, #{{1}\over{x-8}}# se acerca cada vez más a #0#, pero nunca llega a ser igual a #0#. La asíntota horizontal es, por lo tanto, igual a #y=0#.

Or visit omptest.org if jou are taking an OMPT exam.



