Ecuaciones cuadráticas: Desigualdades cuadráticas
Desigualdades cuadráticas
Al igual que con las desigualdades lineales, podemos crear una desigualdad con cuadráticas. Primero veremos cómo resolver una desigualdad cuadrática.
Resolvemos la desigualdad #\blue{2x^2+4x+3} \gt \green{-x^2-2x+6}#.
| Paso 1 | Primero resolvemos la igualdad #\blue{2x^2+4x+3} = \green{-x^2-2x+6}#. Por lo tanto, primero reducimos la igualdad a #0#. \[\begin{array}{rcl}2x^2+4x+3&=&-x^2-2x+6 \\ &&\phantom{xx}\blue{\text{la ecuación por resolver}}\\ 3x^2+6x-3 &=&0 \\ &&\phantom{xx}\blue{\text{reducido a }0} \end{array}\] A continuación aplicamos la fórmula cuadrática. Por lo tanto definimos las letras #a#, #b# y #c#. \[a=3, b=6 \text{ y } c=-3\] A continuación, calculamos el discriminante. \[D=6^2-4 \cdot 3 \cdot -3 =72\] Después de eso, determinamos las soluciones. \[x=\frac{-6-\sqrt{72}}{2\cdot 3} \lor x=\frac{-6+\sqrt{72}}{2\cdot 3} \] Que simplificamos a: \[x=-1- \sqrt{2} \lor x=-1+ \sqrt{2} \] |
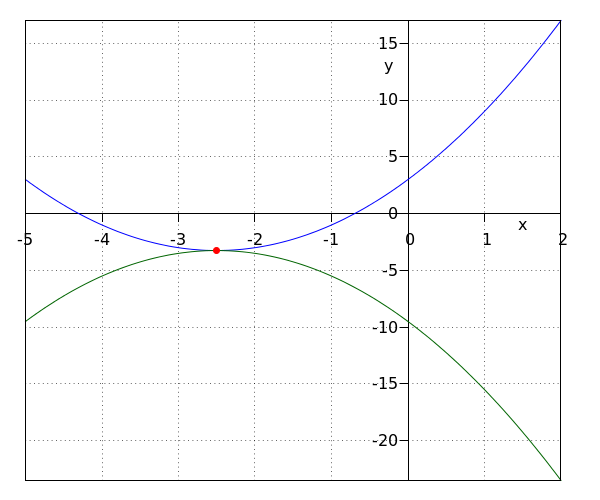
| Paso 2 | Creamos las gráficas de #y=\blue{2x^2+4x+3}# y #y=\green{-x^2-2x+6}#. Los puntos de intersección se dibujan en naranja.  |
| Paso 3 | Determinaremos la solución mediante los pasos 1 y 2. A la izquierda de #x=-1-\sqrt{2}# y a la derecha de #x=-1+\sqrt{2}#, la gráfica de #y=\blue{2x^2+4x+3}# se encuentra por encima de la gráfica de #y=\green{-x^2-2x+6}#. por lo tanto, la solución es #x \lt -1-\sqrt{2} \lor x \gt -1+\sqrt{2}#. |
En general, podemos aplicar el siguiente procedimiento.
Resolver una desigualdad cuadrática
| Procedimiento | ||
| Resolvemos la desigualdad #\blue{a_1 x^2+b_1x+c_1} \gt \green{a_2x^2+b_2x+c_2}#, en la cual #a_1 \ne 0#. |  | |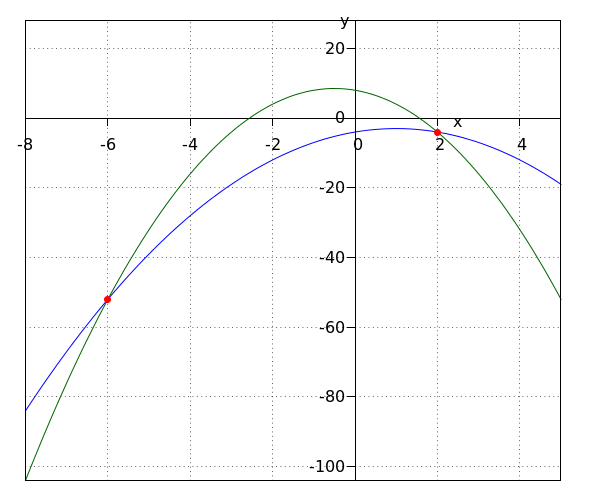
| Paso 1 | Primero resolvemos la igualdad \[\blue{a_1 x^2+b_1x+c_1} = \green{a_2x^2+b_2x+c_2}\] | |
| Paso 2 | Dibujamos las gráficas #y=\blue{a_1 x^2+b_1x+c_1}# y #y=\green{a_2x^2+b_2x+c_2}#. | |
| Paso 3 | Con ayuda de los pasos 1 y 2, determina para qué valor de #x# se cumple la desigualdad. En el sistema de coordenadas, la gráfica más grande es la que está encima de la otra. |
Ten en cuenta que este procedimiento también es válido para los signos de desigualdad #\geq#, pero los valores #x# de los puntos de intersección también son parte de la solución.
Todo o nada
Si no se encuentran puntos de intersección en el paso 1, entonces hay dos opciones con respecto a la solución de la desigualdad.
1) todos los puntos de #x# son una solución de la desigualdad. La desigualdad siempre es verdadera.
2) ningún punto de #x# es una solución de la desigualdad. La desigualdad nunca es verdadera.
Lo mismo ocurre si encontramos un punto de intersección en el paso 1, pero este es un punto de tangencia. Entonces las parábolas son iguales en ese punto y en todos los demás puntos, la desigualdad puede ser verdadera o no.
Ejemplo
Las fórmulas cuadráticas #y=\blue{x^2+5x+3}# y #y=\green{-x^2-5x-\frac{19}{2}}#.
El punto de intersección de las dos fórmulas es #\rv{-\frac{5}{2}, -\frac{7}{2}}#.
La desigualdad #\blue{x^2+5x+3} \geq \green{-x^2-5x-\frac{19}{2}}# es verdadera para todos los puntos de #x#.
La desigualdad #\blue{x^2+5x+3} \lt \green{-x^2-5x-\frac{19}{2}}# no es verdadera para ningún punto de #x#.
| Paso 1 | Resolvemos la igualdad #2\cdot b^2+5\cdot b+6=-3\cdot b^2+6\cdot b+7#. Esto se hace de la siguiente manera: \[\begin{array}{rcl} 2\cdot b^2+5\cdot b+6 &=& -3\cdot b^2+6\cdot b+7\\ &&\phantom{xxx}\blue{\text{la igualdad original}}\\ 5\cdot b^2-b-1&=&0\\ &&\phantom{xxx}\blue{\text{todos los términos se movieron al lado izquierdo}}\\ \text{discriminante } &=& b^2-4ac \\ &&\phantom{xxx}\blue{\text{fórmula discriminante}}\\ &=& \left(-1\right)^2 - 4 \cdot 5 \cdot \left(-1\right) \\&&\phantom{xxx}\blue{\text{fórmula ingresada}}\\ &=& 21\\&&\phantom{xxx}\blue{\text{calculado}}\\ \text{número de soluciones } &=& 2\\&&\phantom{xxx}\blue{\text{ya que el discriminante es mayor que }0}\\ b=\frac{-b-\sqrt{D}}{2 \cdot a} &\lor& b=\frac{-b+\sqrt{D}}{2 \cdot a} \\&&\phantom{xxx}\blue{\text{soluciones de fórmula}}\\ b={{1-\sqrt{21}}\over{10}}&\lor& b={{\sqrt{21}+1}\over{10}} \\&&\phantom{xxx}\blue{\text{fórmula ingresada y calculada}}\\ \end{array}\] |
| Paso 2 | Trazamos las gráficas de #y=2\cdot b^2+5\cdot b+6# (azul) y #y=-3\cdot b^2+6\cdot b+7# (verde).  |
| Paso 3 | Ahora podemos leer la respuesta de la desigualdad. \[b\gt {{1-\sqrt{21}}\over{10}}\land b\lt {{\sqrt{21}+1}\over{10}}\] |
Or visit omptest.org if jou are taking an OMPT exam.
