Ecuaciones cuadráticas: Puntos de intersección de las parábolas
 Puntos de intersección de las parábolas con una recta
Puntos de intersección de las parábolas con una recta
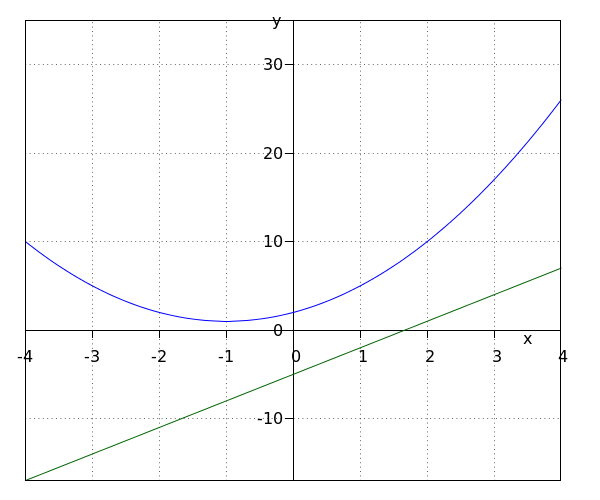
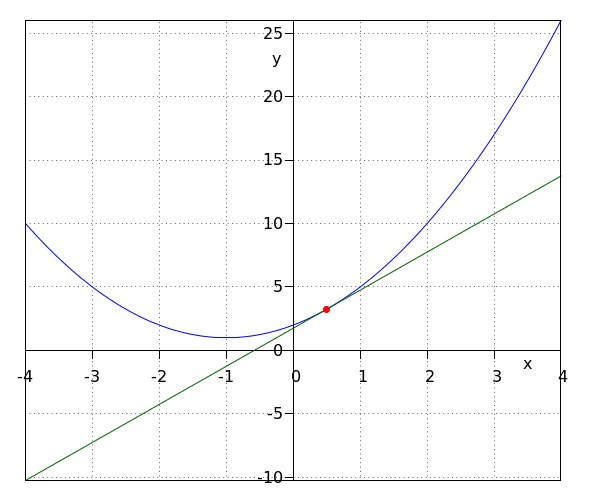
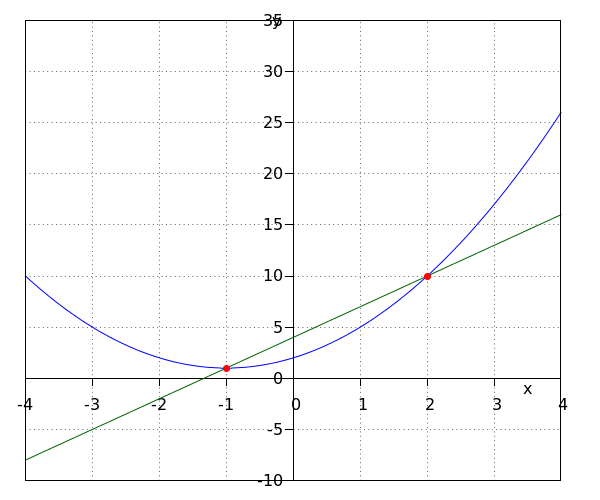
Una fórmula cuadrática #y=a_1x^2+b_1x+c_1# y una fórmula lineal #y=a_2x+b_2# pueden tener cero, uno o dos puntos de intersección. Ahora investigaremos cómo encontrar estos puntos de intersección.
Puntos de intersección de una parábola y una recta
| Procedimiento | geogebra plaatje | |
| Determinamos el punto de intersección de la parábola #y=a_1x^2+b_1x+c_1# y de la recta #y=a_2x+b_2#. | ||
| Paso 1 | Primero determinamos la coordenada #x# del punto de intersección resolviendo la ecuación \[a_1x^2+b_1x+c_1=a_2x+b_2\] por medio de factorización, completando el cuadrado o la fórmula cuadrática. | |
| Paso 2 | Determinamos la coordenada #y# del punto de intersección sustituyendo la coordenada #x# obtenida en una de las dos fórmulas. Por lo general, es más fácil sustituir en la fórmula lineal. |
El último paso indica que dadas las gráficas \[y = -x^2-2\cdot x+8\phantom{xxx}\text{ y }\phantom{xxx} y = x+10\]
se cruzan en dos puntos. Determina los dos puntos de intersección.
Da tu respuesta en la forma de #\left\{\rv{a,b},\rv{c,d}\right\}#, en la cual #a#, #b#, #c#, #d# son números exactos.
se cruzan en dos puntos. Determina los dos puntos de intersección.
Da tu respuesta en la forma de #\left\{\rv{a,b},\rv{c,d}\right\}#, en la cual #a#, #b#, #c#, #d# son números exactos.
#\left \{\rv{ -2 , 8 } , \rv{ -1 , 9 } \right \} #
La coordenada #x# de un punto que se encuentra en ambas parábolas debe satisfacer
\[-x^2-2\cdot x+8 = x+10\tiny.\]
Resolvemos esta ecuación, después de la reducción, por factorización.
\[\begin{array}{rcl}
-x^2-3\cdot x-2 &=& 0\\
&&\phantom{xxx}\color{blue}{\text{todos los términos al lado izquierdo}}\\
x^2+3\cdot x+2 &=& 0\\ &&\phantom{xxx}\color{blue}{\text{links en rechts vermenigvuldigd met -1 }}\\
\left(x+1\right)\cdot \left(x+2\right) &=&0 \\
&&\phantom{xxx}\color{blue}{\text{factorizado}}\\
x+1 = 0 &\lor& x+2=0 \\
&&\phantom{xxx}\color{blue}{A\cdot B=0 \text{ si y solo si }A=0\lor B=0}\\
x=-1 &\lor& x=-2 \\
&&\phantom{xxx}\color{blue}{\text{término constante al lado derecho}}\\
\end{array}\]
Ahora podemos calcular el valor correspondiente #y# ingresando este valor de #x# en una de las dos fórmulas. En este caso lo más conveniente es elegir la función lineal. Primero calculamos el valor de #y# en #x=-2#.
\[\begin{array}{rcl}
y&= & -2+10 = 8
\end{array}\]
A continuación calculamos el valor de #y# en #x=-1#.
\[\begin{array}{rcl}
y&=& -1+10 = 9
\end{array}\]
La conclusión es que los puntos de intersección #2# están dados por: \[ \left \{\rv{ -2 , 8 } , \rv{ -1 , 9 } \right \}\tiny. \]
La coordenada #x# de un punto que se encuentra en ambas parábolas debe satisfacer
\[-x^2-2\cdot x+8 = x+10\tiny.\]
Resolvemos esta ecuación, después de la reducción, por factorización.
\[\begin{array}{rcl}
-x^2-3\cdot x-2 &=& 0\\
&&\phantom{xxx}\color{blue}{\text{todos los términos al lado izquierdo}}\\
x^2+3\cdot x+2 &=& 0\\ &&\phantom{xxx}\color{blue}{\text{links en rechts vermenigvuldigd met -1 }}\\
\left(x+1\right)\cdot \left(x+2\right) &=&0 \\
&&\phantom{xxx}\color{blue}{\text{factorizado}}\\
x+1 = 0 &\lor& x+2=0 \\
&&\phantom{xxx}\color{blue}{A\cdot B=0 \text{ si y solo si }A=0\lor B=0}\\
x=-1 &\lor& x=-2 \\
&&\phantom{xxx}\color{blue}{\text{término constante al lado derecho}}\\
\end{array}\]
Ahora podemos calcular el valor correspondiente #y# ingresando este valor de #x# en una de las dos fórmulas. En este caso lo más conveniente es elegir la función lineal. Primero calculamos el valor de #y# en #x=-2#.
\[\begin{array}{rcl}
y&= & -2+10 = 8
\end{array}\]
A continuación calculamos el valor de #y# en #x=-1#.
\[\begin{array}{rcl}
y&=& -1+10 = 9
\end{array}\]
La conclusión es que los puntos de intersección #2# están dados por: \[ \left \{\rv{ -2 , 8 } , \rv{ -1 , 9 } \right \}\tiny. \]
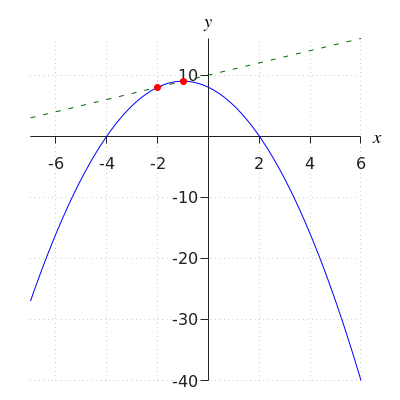
Vemos que los puntos de intersección calculados coinciden con los puntos de intersección identificados en el paso 1. Observa la figura a continuación, en la que los puntos de intersección están dibujados en rojo.

Desbloquear acceso completo


Acceso al profesorado
Solicitar una cuenta de demostración. Le ayudaremos a comenzar con nuestro entorno de aprendizaje digital.
Acceso al alumnado
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.