Ecuaciones cuadráticas: Dibujando parábolas
Intersección de parábolas con los ejes
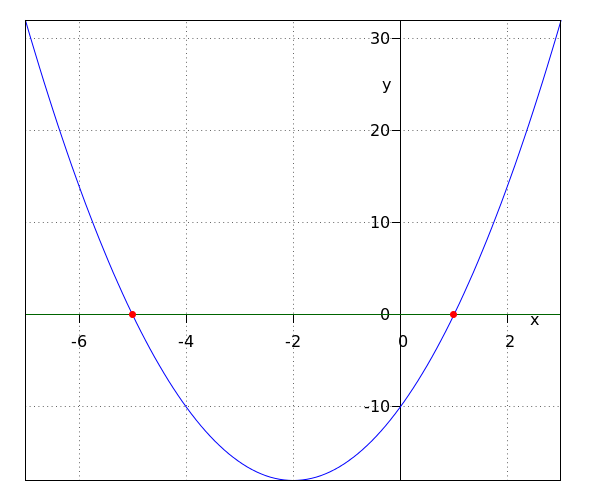
Los puntos de intersección de una parábola con el eje #x# son los puntos a lo largo de la gráfica donde #y=0#.
Para encontrar las coordenadas #x# de estos puntos, debes igualar la fórmula de la parábola a #0# y resolver para #x#:
\[ax^2+bx+c=0\]
Esto se puede hacer por factorización, completando el cuadrado o usando la fórmula cuadrática.
Una parábola puede tener dos, una o ninguna intersección con el eje #x#.
Ejemplo Considera la parábola #y=2x^2+8x-10#.
Las coordenadas #x# de las intersecciones con el eje #x# se pueden encontrar resolviendo la ecuación: \[2x^2+8x-10=0\]
Esto se hace de la siguiente manera:
\[\begin{array}{rcl}2x^2+8x-10&=&0 \\ &&\phantom{xx}\blue{\text{la ecuación por resolver}}\\ x^2+4x-5&=&0 \\ &&\phantom{xx}\blue{\text{dividido ambos lados por }2}\\ \left(x+5\right) \left(x-1\right)&=&0 \\ &&\phantom{xx}\blue{\text{factorizado}}\\x+5=0 &\lor& x-1=0 \\ &&\phantom{xx}\blue{A \cdot B \Leftrightarrow A=0 \lor B=0}\\x=-5 &\lor& x=1 \\ &&\phantom{xx}\blue{\text{se transfirieron las constantes al lado derecho}} \end{array}\]
Entonces las intersecciones de #y=2x^2+8x-10# con el eje #x# son #\rv{-5,0}# y #\rv{1,0}#.
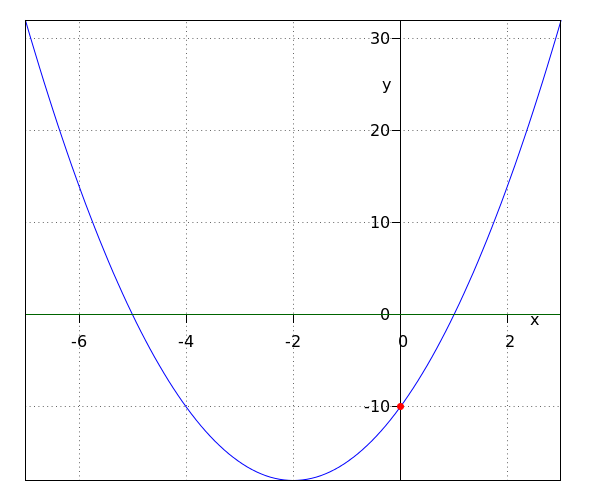
El punto de intersección de una parábola con el eje #y# es el punto a lo largo de la gráfica donde #x=0#.
Una parábola siempre tiene un solo punto de intersección con el eje #y#.
Para encontrar la coordenada #y# de este punto, sustituye #0# por #x# en la fórmula de la parábola.
Una parábola descrita por #y=\blue a x^2+\green b x +\purple c# se cruza con el eje #y# en el punto #\rv{0,\purple c}#.
Ejemplo Considera la parábola #y=2x^2+8x-10#.
Encontramos la coordenada #y# de la intersección con el eje #y# sustituyendo #0# por #x# en la fórmula.
\[y=2 \cdot 0^2+8 \cdot 0 -10=-10\]
Entonces la parábola #y=2x^2+8x-10# se cruza con el eje #y# en el punto #\rv{0,-10}#
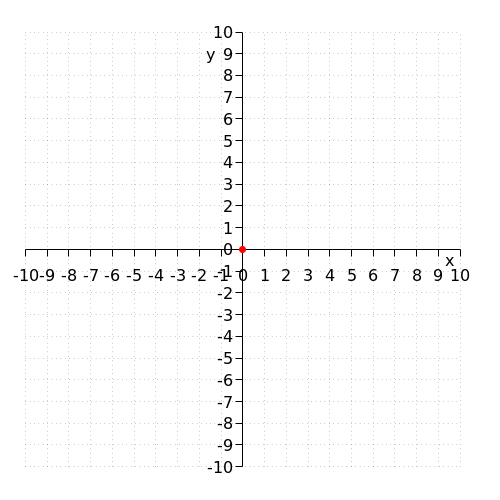
El punto de intersección con el eje #y# es igual al valor de la constante en la función cuadrática: #0#. Por lo tanto, las coordenadas del punto de intersección con el eje #y# son: #\rv{0,0}#.
Or visit omptest.org if jou are taking an OMPT exam.
