Ecuaciones cuadráticas: Dibujando parábolas
 Dibujar parábolas
Dibujar parábolas
Hemos visto que la gráfica de una cuadrática es una parábola. También hemos visto cómo los puntos de intersección con los ejes, el vértice y otros puntos con valores particulares de #x# de la parábola se pueden calcular. A partir de estos valores calculados podemos dibujar fácilmente la gráfica de una cuadrática.
Procedimiento para dibujar una parábola
| Procedimiento | geogebra plaatje | |
| Dibujaremos la gráfica de una cuadrática. | ||
| Paso 1 | Determina el punto de intersección con el eje #y#. | |
| Paso 2 | Determina el vértice. | |
| Paso 3 | Determina los puntos de intersección con el eje #x#, si los hay. | |
| Paso 4 | Sustituye los valores de #x# en la fórmula de tal manera que tengamos al menos 4 puntos que podamos dibujar. | |
| Paso 5 | Dibuja estos puntos en el sistema de coordenadas y conéctalos mediante una parábola fluida. |
Observa la gráfica que pertenece a la siguiente fórmula:
\[y=-{{x^2}\over{5}}-5\cdot x+7\]
Dibuja la intersección con el eje #y#, el vértice y las intersecciones con el eje #x#.
\[y=-{{x^2}\over{5}}-5\cdot x+7\]
Dibuja la intersección con el eje #y#, el vértice y las intersecciones con el eje #x#.
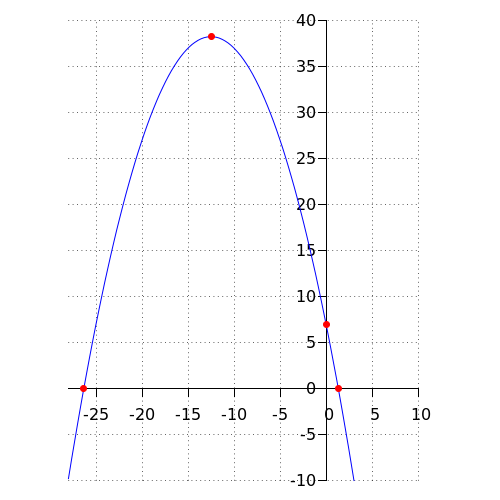
Los puntos rojos son los cuatro puntos de la pregunta. Estos se calculan de la siguiente manera:
La fórmula ya está escrita en la forma de #a \cdot x^2+b \cdot x +c# con #a =-{{1}\over{5}}#, #b=-5# y #c=7#. Se observa como #a<0# la gráfica es una parábola que abre hacia abajo.
La intersección con el eje #y# es igual al valor de la constante en la fórmula cuadrática, que es igual a #7#. Eso significa que las coordenadas del punto de intersección con el eje #y# son #\rv{0,7}#.
El valor de #x# del vértice está dado por #x=-\dfrac{b}{2 \cdot a}# y es igual a:
\[\begin{array}{rclrl}
x&=& -\dfrac{-5}{2 \cdot -{{1}\over{5}}} &&\phantom{xxx}\color{blue}{\text{fórmula ingresada}}\\
&=& -{{25}\over{2}} &&\phantom{xxx}\color{blue}{\text{simplificado}}\\
\end{array}\]
El valor de #y# del vértice se calcula ingresando #x=-{{25}\over{2}}# en la fórmula. Lo que da:
\[\begin{array}{rclrl}
y&=& -{{1}\over{5}} \cdot \left(-{{25}\over{2}}\right)^2 -5 \cdot -{{25}\over{2}} +7
&&\phantom{xxx}\color{blue}{\text{fórmula ingresada}}\\
&=& {{153}\over{4}} &&\phantom{xxx}\color{blue}{\text{calculado}}\\
\end{array}\]
Las coordenadas del vértice son: #\rv{-{{25}\over{2}},{{153}\over{4}}}#. Para dibujar el punto en la gráfica, tenemos que escribir las coordenadas como números decimales (redondeados a 1 decimal). Eso da: #\rv{-12.5,38.2}#.
Las intersecciones con el eje #x# son los puntos que corresponden a #y=0#.
\[\begin{array}{rcl}
-{{x^2}\over{5}}-5\cdot x+7 &=& 0 \\&&\phantom{xxx}\color{blue}{\text{la ecuación que se debe calcular}}\\
x=\dfrac{-{-5}-\sqrt{\left(-5\right)^2-4 \cdot -{{1}\over{5}} \cdot 7}}{2 \cdot -{{1}\over{5}}} &\vee& x=\dfrac{-{-5}+\sqrt{\left(-5\right)^2-4 \cdot -{{1}\over{5}} \cdot 7}}{2 \cdot -{{1}\over{5}}} \\&&\phantom{xxx}\color{blue}{\text{fórmula cuadrática ingresada}}\\
x={{-3\cdot \sqrt{85}-25}\over{2}} &\vee& x={{3\cdot \sqrt{85}-25}\over{2}} \\&&\phantom{xxx}\color{blue}{\text{calculado}}\\
\end{array}\]
Las coordenadas de las intersecciones con el eje #x# son: #\rv{{{-3\cdot \sqrt{85}-25}\over{2}},0}# y #\rv{{{3\cdot \sqrt{85}-25}\over{2}},0}#. Para dibujar el punto en la gráfica, tenemos que escribir las coordenadas como números decimales (redondeado a 1 decimal). Eso da: #\rv{-26.3,0}# en #\rv{1.3,0}#.
Los cuatro puntos de la gráfica son: #\rv{0,7}#, #\rv{-{{25}\over{2}},{{153}\over{4}}}#, #\rv{{{-3\cdot \sqrt{85}-25}\over{2}},0}# y #\rv{{{3\cdot \sqrt{85}-25}\over{2}},0}#.
La fórmula ya está escrita en la forma de #a \cdot x^2+b \cdot x +c# con #a =-{{1}\over{5}}#, #b=-5#, y #c=7#. Como #a<0#, se observa que la gráfica es una parábola que abre hacia abajo .
Los puntos solicitados están conectados por una curva fluida en la figura: la parábola que abre hacia arriba está dada por la fórmula.
Los puntos solicitados están conectados por una curva fluida en la figura: la parábola que abre hacia arriba está dada por la fórmula.
Desbloquear acceso completo


Acceso al profesorado
Solicitar una cuenta de demostración. Le ayudaremos a comenzar con nuestro entorno de aprendizaje digital.
Acceso al alumnado
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.



