Gráficas

Fórmulas y ecuaciones lineales: Fórmulas

Gráficas

Gráfica

Podemos crear una tabla correspondiente a la fórmula #\blue{y=5x+10}#:

\[\begin{array}{l|c|c|c|c|c}
x & 0 & 1 & 2 & 3 & 4\\
\hline
y & 10 & 15 & 20 & 25 & 30
\end{array}\] Hicimos esta tabla calculando el valor de #y# correspondiente al valor elegido de #x# en la fila superior. Los valores de @y@ están en la fila inferior.

Podemos hacer una gráfica correspondiente a esta tabla. La fila superior con valores para #x# corresponde al eje horizontal, y la fila inferior con valores para #y# corresponde al eje vertical.

Si #x=1#, luego #y=15#. Esto corresponde al punto #\rv{1,15}#. A la derecha puedes ver cómo puedes encontrar este punto dibujando líneas perpendiculares desde los ejes. De la tabla se deduce que la gráfica pasa por los siguientes puntos: #\rv{0,10}#, #\rv{1,15}#, #\rv{2,20}#, #\rv{3,25}# y #\rv{4,30}#. Estos puntos están dibujados a la derecha y conectados por una línea perfecta, que en este caso es una línea recta.

Dibuja una gráfica correspondiente a la fórmula:
\[y=-3\cdot x\]

En primer lugar, construiremos una tabla correspondiente a la gráfica. Para esto, sustituimos los valores #x# en la fórmula. Para #x=-4# encontramos #y=\left(-3\right)\cdot \left(-4\right)=12#. Los otros valores #x# siguen el mismo patrón. Finalmente encontramos la tabla a continuación.

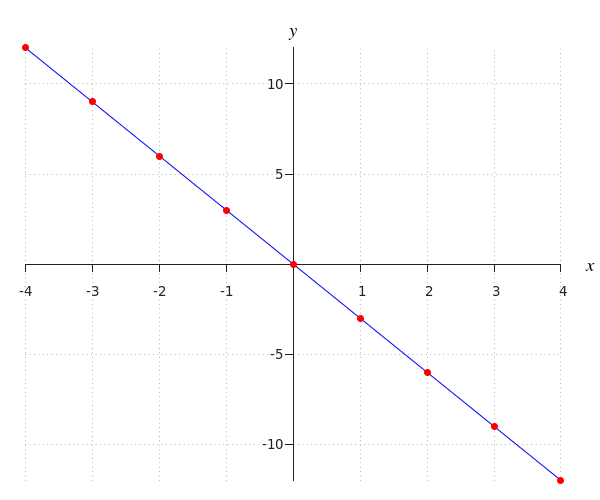
#\boldsymbol{x}#	#-4#	#-3#	#-2#	#-1#	#0#	#1#	#2#	#3#	#4#
#\boldsymbol{y}#	#12#	#9#	#6#	#3#	#0#	#-3#	#-6#	#-9#	#-12#

Para construir la gráfica, dibujamos un sistema de coordenadas. Luego, dibujamos los puntos de la tabla en el sistema de coordenadas, porque estos son puntos en la gráfica. El valor #x# está en el eje horizontal y el valor #y# está en el eje vertical. Luego, conectamos estos puntos con una curva perfecta. Esto nos da la siguiente gráfica. Los puntos de la tabla están coloreados en rojo.

Nuevo ejemplo