Fórmulas y ecuaciones lineales: Ecuaciones lineales y desigualdades
Punto de intersección de dos fórmulas lineales
Hemos visto cómo resolver una ecuación lineal. Con esta misma técnica también podemos determinar las coordenadas de los puntos de intersección de dos fórmulas lineales.
Consideramos las fórmulas lineales #\blue{f: y =2 \cdot x + 5}# y #\green{g: y=-3 \cdot x -4}#. Podemos encontrar la coordenada #x# del punto de intersección resolviendo la ecuación #2 \cdot x +5=-3 \cdot x-4#. Esto se hace de la siguiente manera:
\[\begin{array}{rcl}2 \cdot x +5&=&-3 \cdot x-4 \\ &&\qquad\blue{\small\text{la ecuación}} \\ 5 \cdot x +5&=&-4 \\&& \qquad \blue{\small\text{ambos lados más }3 \cdot x} \\ 5 \cdot x &=&-9 \\ &&\qquad\blue{\small\text{ambos lados menos }5}\\x&=&-\dfrac{9}{5}\\ &&\qquad\blue{\small\text{ambos lados divididos por }5} \end{array}\]
Por lo tanto, la coordenada #x# del punto de intersección es #x=-\tfrac{9}{5}#.
Podemos encontrar la coordenada #y# sustituyendo #x=-\tfrac{9}{5}# en una de las fórmulas. Esto nos da: \[y=2 \cdot -\tfrac{9}{5}+5=\tfrac{7}{5}\] Por lo tanto, las coordenadas del punto de intersección son #\rv{-\tfrac{9}{5}, \tfrac{7}{5}}#.
Punto de intersección de dos fórmulas lineales
La coordenada #x# del punto de intersección de las dos fórmulas lineales #y=a \cdot x+b# y #y=c \cdot x +d# es la solución de la ecuación #a \cdot x+b=c \cdot x+d#. La coordenada #y# se puede encontrar sustituyendo la coordenada #x# encontrada en una de las fórmulas lineales.
Después de todo, en la siguiente gráfica, el punto de intersección está dibujado en verde.
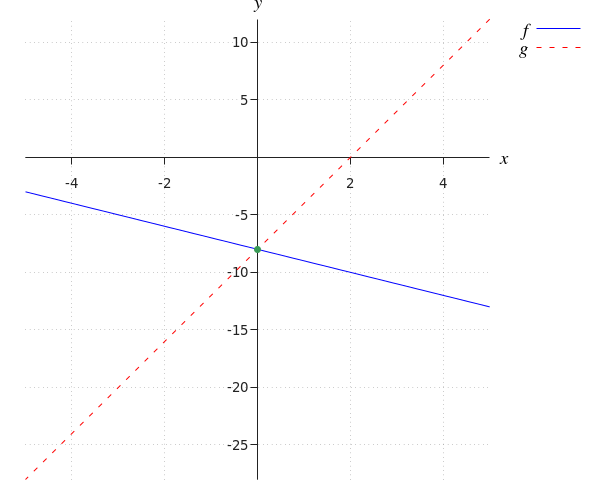
Podemos ver que la coordenada #x# del punto de intersección es igual a #0#. La coordenada #y# del punto de intersección es igual a #-8#.
Por lo tanto, el punto de intersección es: #\rv{0, -8}#.
Or visit omptest.org if jou are taking an OMPT exam.
